コラム
デジタル社会形成に向けて 第2章(11)~自治体DXの先に~
2022.12.05
訪問型行政サービスの効果測定を下記フローに沿って説明してきております。(下図記載)
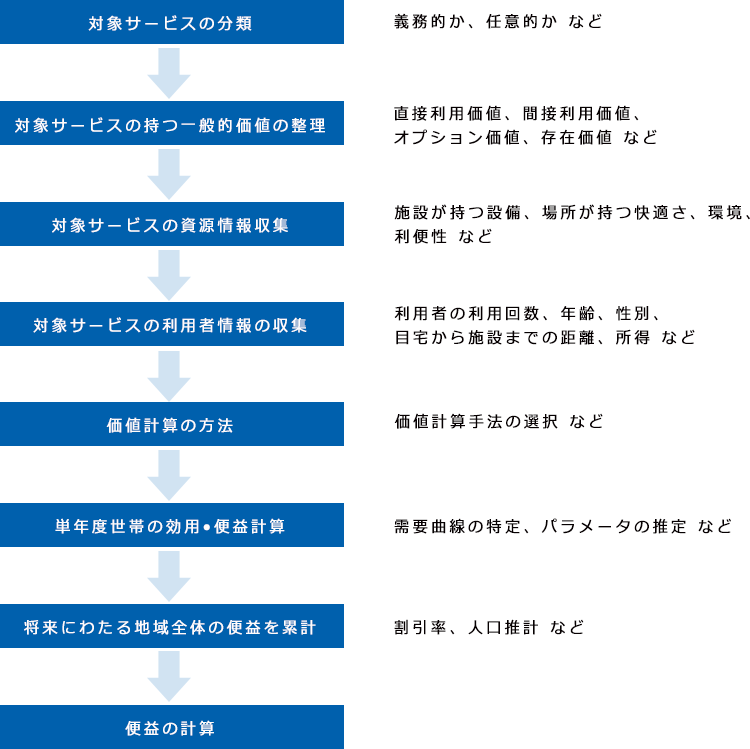 図1:訪問型行政サービスにおける効果測定フロー
図1:訪問型行政サービスにおける効果測定フロー
前回からの続き~変数間の相関
前回のコラムにおいて、クラス分けが終わり、いよいよ施設利用を説明するための変数に関して、中身に関する議論を始めるところになります。ここでいう変数というのは、施設利用者の属性と施設の属性のことでした。前者については、「年齢」「所得」「仕事」「自宅から施設までの距離」など、後者については、施設の「規模」「簿価」「経年」などを指します。
我々が知りたいのは、これら各変数が公共施設の選択行動に影響を与えているかどうか?また、与えているとしたら、どの程度の影響力があるのか?という点です。この点が分かれば、より「消費者ニーズ」に沿った形でサービスを提供できるようになるでしょう。民間ではごく当たり前のように行われている「マーケティング」に通じる話です。もっとも、民間サービスの場合は、供給側の利益極大化と需要側の効用最大化の交差点で「価格と取引量」が決まるという、例の話が有りますが、公共サービスでは、また、別の原理が作用します
「利用者の選択行動を説明できる変数」のことを説明変数と呼ぶことがあります。また、説明される側の変数は被説明変数、または、目的変数と呼ばれます。この「説明できる」というところが微妙で、必ずしも「Aが起きると必ずBが起きる」といった因果関係と同値ではありません。ある程度安定的に一定の関係が見られる、つまり相関があるということです。
相関というのは、普段の会話でも「関係がある」という意味で使われます。では、関係があるとはどういうことか?基本は2つの変数間の話になります。3つ以上の変数を同時に関係定義するのは大変ですので。例えば、下図2のようなデータが示されていると致しましょう。
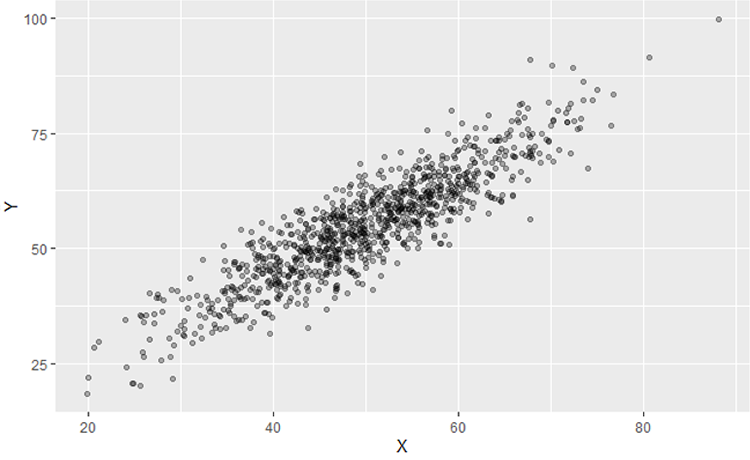 図2:相関係数
図2:相関係数
何か適当な2変数について、片方をx軸方向に、もう片方をy軸方向として、交点をプロットしたものになります。何となく右上がりで、かつ、直線的な雰囲気が感じられます。右上がりということは、xが大きいとyも大きいということです。xが大きくなると、yが小さくなる場合は、右下がりの関係になります。この様な2変数の絡まり具合を「線形」として認識しようというのが相関であり、その(直線的な)絡まり具合を数値化したのが「相関係数」です。
2つの変数間に限定して、取り敢えず「直線的」な関係に絞って考えましょう、という話をしましたが、複雑な関係もありえます。
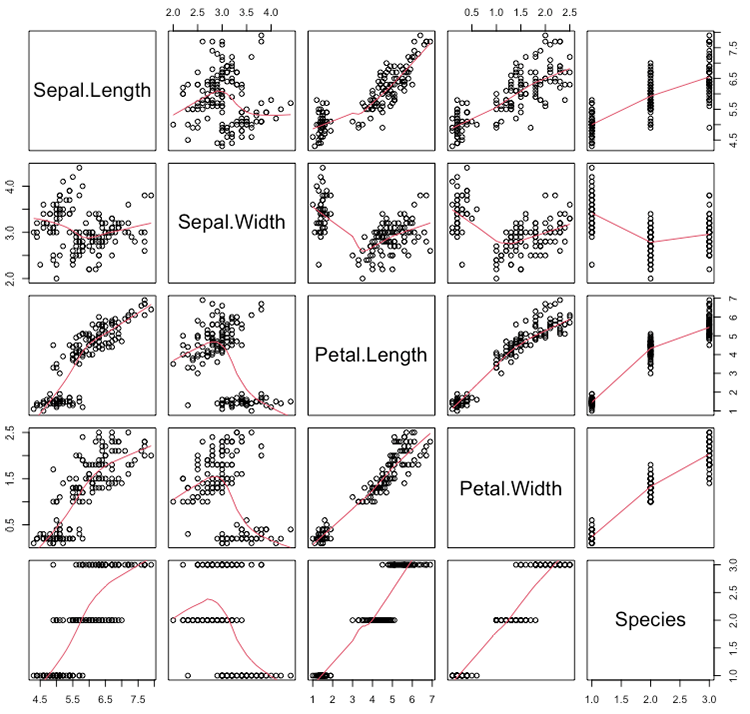 図3:相関関係一覧
図3:相関関係一覧
複雑な関係とはどのようなものか?上記図3をご覧下さい。これは統計分析ソフトウェア「R」の統合開発環境「R studio」に用意されているiris(アイリス;あやめ)というデータセットに入っている変数を抜き出して、総当たりで相関関係を図示したものです。Sepalというは「がく片(※1)」、Petalというのは「花びら」、Speciesというのは「種類」です。このデータセットには、あやめに関する種類別・部位別の観測データ(長さや幅)が入っているということです。
図3には、Sepal.Length、Sepal.Width、Petal.Length、Petal.Width 、Speciesという5つの変数が登場しています。これらの変数をそれぞれ縦軸・横軸にとって、縦横の軸を入替えながら、2変数相互の交点をプロットすると、上記の図が20枚出力されます。自分と自分の関係をプロットしても仕方無いので、それらは左上から右下に伸びる対角線として、文字だけで図は表示されていません。図を見ると、それぞれ面白いデータのバラツキが観測されています。図中に赤線が引いてありますが、これは何となくこんな傾向?ということで、自動的に加えられています。直線に近いものから、2次曲線・3次曲線のように曲がっているのもあります。
このように「非直線」で2変数間の関係を定義することも可能ですが、解釈が難しくなります。直線的な関係ならば「四則演算」の世界で処理できます。それが曲線関係になってしまうと、ある変数xが1単位動いた時に相関する変数yの動き方は、曲線の所々で違ってしまいます。
相関係数について
2変数の直線的な関係に絞って定義されるのが相関係数です。2変数が完全に一致すると1、完全に一致しないとゼロになります。また、完全に「真逆」に関係すると、-1になります。数式ではなく言葉で表現すると
「分子:変数xと変数yの共分散(偏差の積和の平均)を、分母:変数xと変数yの、それぞれの標準偏差の積として、分子/分母で求める」
という事になります。
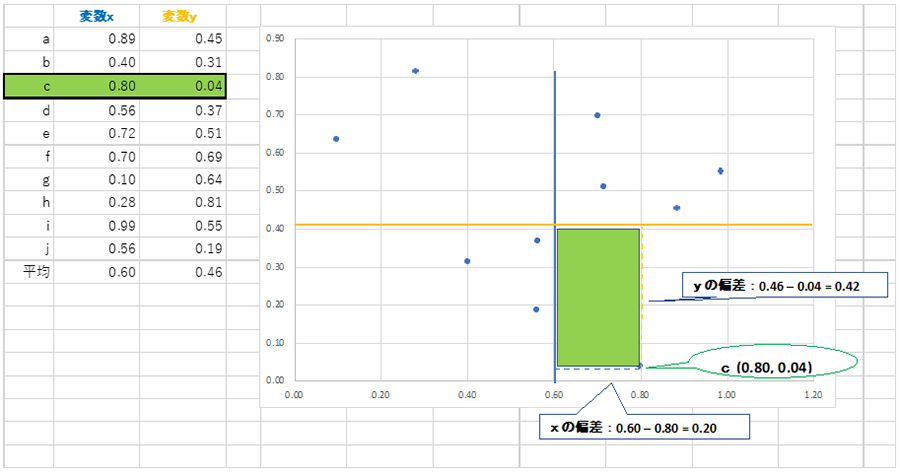 表1:相関係数
表1:相関係数
上記表1のとおり、計算自体はExcel等で行うことができます。分子の「偏差の積の和の平均」というのが、分かり難いかも知れませんが、順番になぞっていくと、意外にそうでもありません。
最初に、変数xと変数yを取ります。サンプルサイズは10で、a〜jまで名前を付けてあります。変数xの平均は0.6、変数yの平均は0.46となっております。ここで点cに注目すると、変数xは0.80、変数yは0.04となっております。それぞれの偏差(平均からの差分)を求めると、0.60 – 0.80 = 0.20、0.46 – 0.04 = 0.42となります。符号は取り敢えず無視し、それぞれの偏差を求めます。次は「積」ですが、これは色塗り長方形部分の面積になります。続いて「和」です。上記表1では、点cの例を表示していますが、点a〜j全ての面積計算を行い加算します。最後は「平均」ですが、上記で算出した10個分の面積合計をサンプルサイズの10で割ります。
これが分子の正体です。実際には符号が付いているので、単純に「面積」ではありませんが、イメージは掴めたはずです。分子の説明で手間取りましたが、次回以降は、分母の説明をする事で「相関」深堀していきます。
(以上)
コラムニスト
公共事業本部 ソリューションストラテジスト 松村 俊英
参考
- ※1萼(がく)片
植物の花を構成する組織で、花を保護する働きを持つ「がく」のひとつひとつを指す。
関連コラム
- デジタル社会形成に向けて 第2章(1)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(2)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(3)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(4)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(5)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(6)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(7)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(8)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(9)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(10)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(11)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(12)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(13)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(14)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(15)~自治体DXの先に~
- 「データ分析を考える」コラム一覧に戻る
