コラム
木も見て森も見たい(13)~公共資本ストックと地価に関係はあるか~
2021.04.26
前回からの続き
前回のコラムにおいて、統計的検定という、ある種不思議な、でもよく考えられている手法を概観致しました。ある変数Xが持つ、Yという変数に対する説明力を確かめるために、確率的に分布する誤差項の存在を仮定し、この誤差項ε(エプシロン)を最小化するために、最小自乗法を使って計算されたXの係数がβです。
βはその出自からして、確率変数です。その確率分布は正規分布であると想定し、今回計算されたβの値が、正規分布のどの辺に位置するかを確かめるために、仮に平均値をゼロとして、t値を計算してみる事にします。
t値はどれくらいなら良いのか?
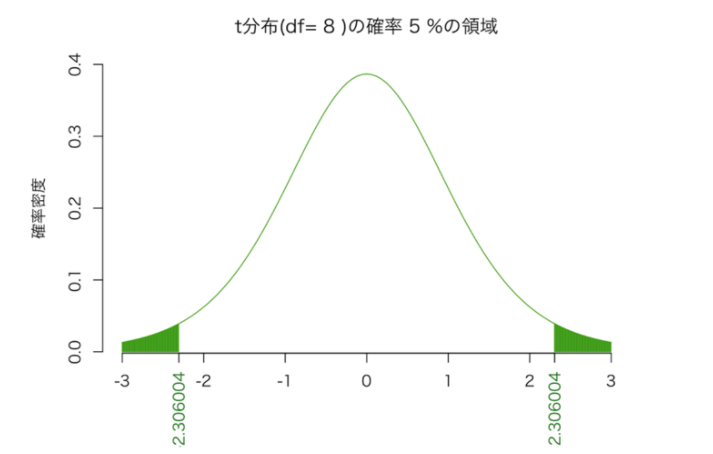
t分布は釣り鐘状の分布なので、このt値が大きな値になっていれば、それは、t分布の左右に拡がる裾野のどこかにプロット(描画)されるはずです。
釣り鐘状に拡がる確率分布の裾野の部分は、確率的に滅多に起きないエリアとなる。すなわち「t値が大きい=端の方に位置する=滅多にないことが起きている。」そんな事象が起きるのは、「平均値をゼロ=βをゼロと考えた前提が間違っている。」そのため、前提条件が棄却され、βはゼロではないと説明できる、と。一気に説明致しましたが、実際にt分布がどういうものかをご覧になっていただきたいのです。
では、実際の例を見ると、下記の通りになります。
データ一覧の集計で使用したコード▼
df <- 8
p <- .05
curve(dt(x, df), from=-3, to=3, bty=”n”, xlab=””, ylab=”確率密度”, col=”#339900″,
main=paste(“t分布(df=”, df, “)の確率”, round(p*100, 2), “%の領域”))
segments(x0 <- seq(-3, q0 <- qt(p/2, df), by=.01), 0, x0, dt(x0, df), col=”#339900″)
segments(x1 <- seq(q1 <- qt(1-p/2, df), 3, by=.01), 0, x1, dt(x1, df), col=”#339900″)
axis(side=1, at=c(q0, q1), col.axis=”#006600″, cex=0.8, las=2)
正規分布でも同じですが、曲線で囲まれた部分の面積を確率と考えることができます。全体の面積が1(=100%)になります。ヒストグラムの階級(横軸を区切る単位)が、細かくなっていくイメージを想像頂くと解りやすいでしょう。
t分布の両裾は、滅多に起こらない領域です。すなわち、起こる確率が低い。この両裾を、仮に片側から2.5パーセントずつ(両側合計で5%)カットするとした場合、その時カットされた部分のt値を読むと、絶対値でだいたい2程度になっていると思います。従って、回帰分析をした場合、「t値の絶対値がだいたい2よりも大きければ一安心」と言われるのは、その所以です。このように、t分布の両側合計で5%の面積を捨て去る部分と仮定して、得られたt値、すなわち、βの説明力があるかどうかを検定する水準ですが、「95%の有意水準」と言われます。有意水準は、99%や90%が設定されることもあります。
「95%で有意」とは、日常生活では使われることがない言い回しですが、これは「100回もβのサンプルを取って来たら、5回くらいは外れ値も出るさ。間違える時もあるが、それは許容範囲内である。」という、ある種の達観でもあります。もちろん、医療など人命が掛かっている分野においては、達観しているだけでは済まされないこともあります。そんな場合は、最も厳しい99%水準(非常に稀なケースとして、1%の外れ値が出るかも)を設定することが多いのではないでしょうか。
この「外れ値が出るかも?」という確率(棄却域)は、「p値」として表現されることもあります。標準正規分布やt分布は、既に分布の中心から端の方にどれ位行けば何%になる、というのは全部分かっています。つまり、t値がいくらだったらp値はいくら、という関係が分かっています。そこで、説明変数Xの説明力を検定する際には、p値を確認して5%以上なのか、あるいは5%以下なのか、という具合に議論されることになります。
ということで、データ分析のお話をしてきまして、最後は統計的検定の話になりました。最初にハードルを上げてパネルデータで分析を始めたため、「お。では、固定効果と変量効果とか、その辺の話をやるのだろうか?」と期待されていた方もいたかもしれません。本来であれば、そういったお話まですべきだったのでしょうが、更に込み入った話になってしまいますので、稿を改めさせて頂きたく。
あとがき
本来ならば、統計分析に関するコラムの開始時点でお話すべきことだったのですが、データを入手したとき、とりあえずデータを集計してみる、という業務がよく発生するかと思います。多くの方は、Excelのピボットテーブルをお使いになるか、本格的にデータを集計・分析される方は、BIツールを用いて、分析されていらっしゃるかもしれません。
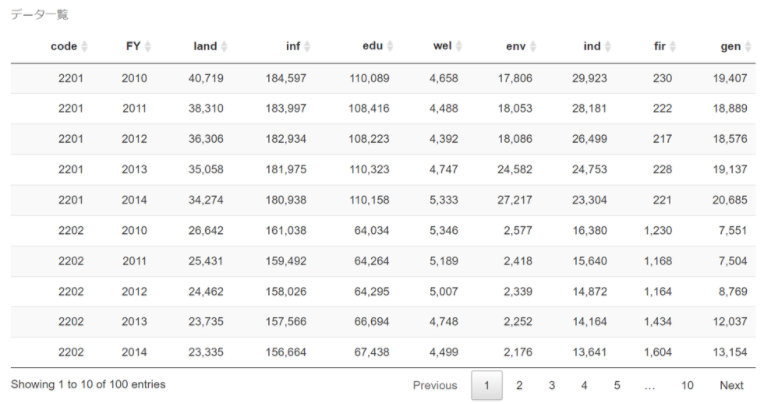
実は、これまで統計分析に使ってきたRにも、お手軽にピボットテーブルの様な操作を可能にするライブラリが提供されております。唐突感は否めませんが、どんな感じになるか、下記にお示しします。データセットは、今まで分析に使ってきたバランスシートのデータになります。ただ、そのままだと容量が大きいので、ここではサンプルとして最初の100レコードだけを抜粋してありますので、最後になりましたが、ご覧になっていただければ幸いです。
データ一覧
データ一覧の集計で使用したコード▼
#パッケージの読み込み
library(psych)
library(rpivotTable)
# ディレクトリの指定
setwd(“/Users/tm/Dropbox/_Study/Ebisu/”)
# データの読み込み
# View(fs_data)
fs_data <-
read_csv(“./200907_fs_data.csv”) %>%
# 名称変更、正規化せず
rename(land = 4, inf = 5, edu = 6, wel = 7, env = 8, ind = 9, fir = 10 ,gen = 11) %>%
# ゼロデータを削除
filter(code != 13102) %>%
# 合計値を挿入
# nest(inf : gen) %>%
# mutate(total = map_dbl(data, ~ sum(.))) %>%
# unnest(data) %>%
select(-1) %>%
slice(1 : 100)
# データ一覧
fs_data %>%
datatable(
caption = “データ一覧”,
rownames = F) %>%
formatCurrency(columns = c(3 : 10), currency = “”, mark = “,”, digits = 0)
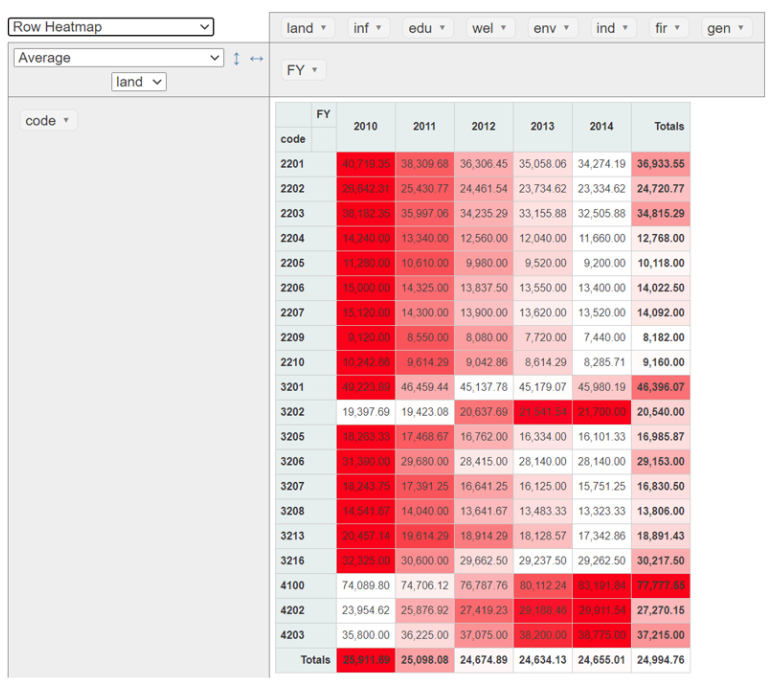
上記のデータを読み込んで、ピボットテーブルの形で表現することもできます。画像では縦軸に自治体コード、横軸に年度を取って、地価=landを並べ替えてみました。「ヒートマップ」という表現を選んでいるので、数値が大きいほど赤い色が濃くなっております。ただ並べ替えただけなので「ふ~ん」という感じかも知れませんが、ドラッグ&ドロップで軸を入れ替えたり、表現を変えたり出来ます。色々と試してみてください。こんなツールでは物足りないという方は、是非本格的なツールにチャレンジしてみて下さい!
ピボットテーブル

コラムニスト
公共事業本部 ソリューションストラテジスト 松村 俊英
関連コラム
- 木も見て森も見たい(1)~自治体財務データから見えるもの
- 木も見て森も見たい(2)~自治体財務データから見えるもの
- 木も見て森も見たい(3)~自治体財務データから見えるもの
- 木も見て森も見たい(4)~自治体財務データから見えるもの
- 木も見て森も見たい(5)~自治体財務データから見えるもの
- 木も見て森も見たい(6)~自治体財務データから見えるもの
- 木も見て森も見たい(7)~公共資本ストックと地価に関係はあるか
- 木も見て森も見たい(8)~公共資本ストックと地価に関係はあるか
- 木も見て森も見たい(9)~公共資本ストックと地価に関係はあるか
- 木も見て森も見たい(10)~公共資本ストックと地価に関係はあるか
- 木も見て森も見たい(11)~公共資本ストックと地価に関係はあるか
- 木も見て森も見たい(12)~公共資本ストックと地価に関係はあるか
- 木も見て森も見たい(13)~公共資本ストックと地価に関係はあるか~
- 「データ分析を考える」コラム一覧に戻る
